SEMANA 11 - MURO DE CORTE

MUROS DE CORTE

El muro de corte es un elemento que se comporta de una manera muy rígida lo que evita excesivos desplazamientos en su dirección más larga; Se colocan diafragmas porque estos resisten gran parte del cortante por planta. Y como ya se ha dicho evitan desplazamientos excesivos.

El muro de corte es un elemento que se comporta de una manera muy rígida lo que evita excesivos desplazamientos en su dirección más larga; Se colocan diafragmas porque estos resisten gran parte del cortante por planta. Y como ya se ha dicho evitan desplazamientos excesivos.

La eficiencia de los muros de corte para restringir las deformaciones laterales disminuye con la altura. Se puede controlar mediante una combinación adecuada de muros y pórticos, al combinar los pórticos con los muros, el muro toma una parte importante del cortante en los primeros pisos y el pórtico lo toma en los pisos superiores.

Como se puede ver en los gráficos anteriores tiene mayores ventajas usar sistemas pórtico – muro los cuales ayudan a la estructura a no sufrir grandes deformaciones que podrían exceder su resistencia a la cual fue diseñada.

Los muros de corte son aquellos que además de las cargas verticales, también reciben cargas horizontales paralelas a su plano, principalmente provenientes de solicitaciones sísmicas. En nuestro medio son conocidos como “placas” y en edificios altos su uso es fundamental, ya que aportan rigidez lateral ayudando a controlar los desplazamientos durante un evento sísmico.

ANÁLISIS ESTRUCTURAL

Al igual que las vigas, los muros de corte se modelan como parte de pórticos; y las cargas sísmicas también se obtendrán del modelo estructural usado para el análisis sísmico. Una vez obtenidas las cargas sísmicas y de gravedad, se procede a resolver todas las combinaciones que establece la Norma E.060.

v U = 1.4 CM + 1.7 CV

v U = 1.25 (CM + CV) ± CS

v U = 0.9 CM ± CS

La mayoría de los muros de corte reciben momentos mayores en una dirección  X-X pero es necesario revisar la sección menos cargada. Es conveniente analizar cada dirección por separado, y obtener las combinaciones de carga respecto a cada eje. A diferencia de las vigas, no se trabaja con una envolvente, sino se estudia cada combinación por separado.

Debido a que tienen que soportar fuerzas debido a cargas que actúan perpendicular y paralelamente a sus caras. Su comportamiento puede variar porque pueden estar sometido a cargas en toda su longitud pero si se aplica una fuerza puntual se considera que solo esa porción soporta la fuerza. 

1.   CLASIFICACION DE LOS MUROS DE CORTE

A.   Por su esbeltez

La esbeltez de un muro se cuantifica por la relación K = H / L, llamada relación de esbeltez; cuando esta relación es mayor a 2 el muro se clasifica como largo o esbelto; por el contrario cuando K ≤ 2 el muro se clasifica como corto o bajo. En los muros esbeltos la resistencia a la flexión controla el comportamiento del muro, mientras que en los bajos el cortante controla las deformaciones de flexión y la resistencia. Los muros esbeltos pueden diseñarse como muros dúctiles para darles buenas características de disipación de energía ante cargas cíclicas reversibles.

           B.    Forma de sección transversal

Los muros pueden ser de forma rectangulares, sección T, L o U, y otras formas más elaboradas, en algunas ocasiones el muro tiene ensanchamiento en sus extremos los cuales se construyen para permitir el anclaje de vigas transversales, para colocar su refuerzo a flexión

              Por su forma en elevación

La mayoría de los muros de corte no sufren cambios en las dimensiones en su elevación, la dimensión que cambia con frecuencia es el espesor, cuando los muros de corte deben tener en su interior ventanas o puertas se les llama muros con aberturas.

          ESTRUCTURAS CON MUROS DE CORTE

a)    Ubicación de los muros:

Los muros individuales generalmente actúan como voladizo, en el diseño sismorresistente se esperan deformaciones dentro del rango no lineal lo que exige una buena distribución de los muros en planta del edificio. Si se utilizan pocos muros concentrándolos en lugar de distribuirlos, las demandas de ductilidad pueden resultar excesivas con la consecuente pérdida de resistencia.

        MUROS ESTRUCTURALES ESBELTOS

a)    Tipos de Fallas y Criterios de Diseño

Estos tienen relación de esbeltez mayor a 2, lo que permite que su mayor fuente de disipación de energía.

Como el área transversal del muro es demasiado grande, tiene alta capacidad para soportar cargas axiales y por consiguiente las cargas que actúan sobre el estarán muy por debajo de la capacidad en condiciones balanceadas, debido a lo anterior se obtiene una adecuada ductilidad si:

ü  Se coloca el refuerzo por flexión en los extremos de los muros.

ü  Se confinan los extremos de muros con estribos con bajas separaciones, para aumentar así el confinamiento de la albañilería y reducir la posibilidad del pandeo del fuerzo a flexión.

Para que no ocurra una falla por cortante:

ü  El agrietamiento por tensión diagonal no se presente antes que se presente los momentos máximos que puede soportar el muro y que generan la falla por flexión.

ü  Las tensiones máximas de trabajo de los muros a cortante debe mantenerse bajas para evitar las fallas por aplastamiento y deslizamiento del muro.

                              I.        Resistencia a la flexión

Para este tipo de muro que se diseña como los esbeltos se coloca el refuerzo vertical a flexión en las partes extremas de la sección transversal que le da una mayor resistencia y mayor ductilidad.

                            II.        Resistencia al Corte

La resistencia que se agrega es considerable a la que se puede obtener de las vigas con la diferencia es que la altura efectiva de la sección “d” para el caso de muros se toma 0.80L.

El refuerzo debe colocarse en el alma del muro y el refuerzo debe ser de diámetro pequeño y separaciones cortas, para asegurar  la resistencia al agrietamiento diagonal del concreto es necesario colocar una cuantía mínima de refuerzo horizontal para acero con

fy = 4200 Kg/cm² la cual será del 25% de la mínima la cual es suficiente para controlar los efectos de temperatura y fraguado.

Para el desplazamiento por cortante en muros esbeltos es menos crítico que  el caso de vigas debido a la carga axial que tiene y a la distribución uniforme del refuerzo vertical que ayuda a evitar el agrietamiento horizontal.

Aunque el muro se confine es posible que falle por inestabilidad lateral para evitar el pandeo fuera del plano se usa para los casos en que la relación de esbeltez es  H libre/b ≤ 14 o 10.

         MUROS ESTRUCTURALES CORTOS O BAJOS

a)    Clase de Muros Cortos

Se considera para la relación de esbeltez H/L ≤ 2 y de acuerdo a su comportamiento se puede clasificar en:

ü  Muros Elásticos: Como la resistencia de los muros cortos es tan alta es normal que respondan aun ante sismos intensos, dentro de un intervalo elástico por lo cual su uso es el más frecuente.

ü  Muros que  Cabecean: Son los que soportan la mayor carga lateral y una carga vertical relativamente baja, en este caso su resistencia esta dado para no poder voltearse si se diseña para este tipo el comportamiento del muro será elástico.

ü  Muros Dúctiles: Diseñados para que trabajen bien en el estado inelástico en el que puedan producir alguna carga.

Para este tipo de muro la flexión es más alta ya que es difícil desarrollarlas sin que antes falle por cortante que es dada por la ductilidad es mucho menor que la requerida para muros esbeltos los cuales son de ductilidad restringida.

b)    Resistencia a la Flexión

Para que soporten el momento flector se usa el refuerzo vertical mínimo, el problema que tiene es como resistir las fuerzas cortantes, al igual que para muros esbeltos, la distribución del acero uniformemente ayuda a resistir los deslizamientos cortantes que pueda presentarse.

Para determinar la cantidad de acero que se debe distribuir en el diafragma se toma de la siguiente ecuación:

As = ρ.h.t.H

c)    Resistencia al Cortante

Como se vio en los muros de corte esbeltos es indispensable la colocación de refuerzos horizontales para resistir parte de la fuerza cortante. Sin embargo también es necesario colocar el refuerzo vertical para tomar el cortante. Al igual que para los muros esbeltos la cuantía mínima es del 0.25% para refuerzo vertical.

La falla por compresión o tensión diagonal se evita si se limita la tensión cortante y se coloca refuerzo horizontal para evitar fallar por aplastamiento.

REFUERZO MÍNIMO HORIZONTAL Y VERTICAL

Dadas las importantes dimensiones que presentan los muros de corte, la Norma E.060
especifica cuantías mínimas de refuerzo para evitar la fisuración. En su artículo 11.3 señala:

Estos mínimos aplican siempre y cuando no se requiera cuantías mayores por corte. El
espaciamiento no debe ser mayor a tres veces el espesor del muro, ni 40 cm. Si el espesor es
mayor a 20 cm, el refuerzo debe estar repartido en ambas caras del muro. El refuerzo vertical
no necesita estar confinado salvo que su cuantía exceda de 0.01.

DISEÑO POR FLEXIÓN

De acuerdo a la esbeltez del elemento, su comportamiento por flexión varía notablemente, por
consiguiente el diseño del refuerzo vertical por flexión debe diferenciarse para dos casos:

 Muros esbeltos (H/L ≥ 1)

En muros esbeltos el comportamiento es similar al estudiado para el caso de columnas, donde las fallas más probables son las del tipo dúctil, debido a la formación de rótulas plásticas en la base. El diseño se realizará por flexocompresión.

Se asume el acero principal en los núcleos confinados y el acero repartido en el resto de la sección. Se ubican los núcleos confinados en los extremos y donde se presenten vigas o
muros perpendiculares al plano del elemento. Por último, se elaboran los diagramas de
interacción para cada dirección y se ubican los puntos (Mu,Pu) para comprobar la validez de la iteración.

Muros bajos (H/L < 1)

En estos casos la falla más probable es del tipo frágil, por tracción diagonal del        elemento, por lo tanto la fuerza cortante gobierna el diseño. El     comportamiento          no corresponde a la de un elemento sometido a flexocompresión y es semejante al de    una viga de gran peralte.

Para calcular el acero de refuerzo del extremo en tracción para secciones rectangulares       podrá calcularse con la siguiente expresión (Blanco, 1994). 

DISEÑO POR CORTE

La Norma E.060 en su artículos 11.10.3 a 11.10.10, indica las consideraciones para el diseño del refuerzo por corte en placas.

El aporte del concreto se puede calcular mediante las siguientes expresiones, considerando la magnitud de la carga axial.

Donde es el espesor del muro y el peralte efectivo, el cual deberá ser calculado mediante un análisis de compatibilidad de deformaciones, sin embargo la Norma E.060 permite el uso de d=0.8L.

Además la Norma E.060 señala algunos límites para las resistencias calculadas.

Donde αc varía linealmente para valores intermedios de H/L. Además se especifica
un límite para el valor de Vn=Vc + Vs, según la siguiente expresión.

La Norma E.060 indica que no es necesario considerar la cuantía de refuerzo vertical mayor que la horizontal, salvo que la relación sea menor a 2, en cuyo caso es sí será necesario considerar que ρv ≥ ρh. Para los espaciamientos, tanto vertical como horizontal, se debe cumplir que:

Adicionalmente la Norma E.060 en su artículo 21.9.5.3, referente a las disposiciones para el diseño sísmico de muros estructurales, señala que la fuerza cortante de diseño debe ajustarse a la capacidad en flexión instalada en el muro:

EMPALMES POR TRASLAPE DEL REFUERZO

Los núcleos confinados se pueden considerar individualmente como columnas, por
consiguiente los empalmes se pueden especificar de acuerdo con lo dispuesto en la sección referente a columnas.

 EJEMPLO DE DISEÑO

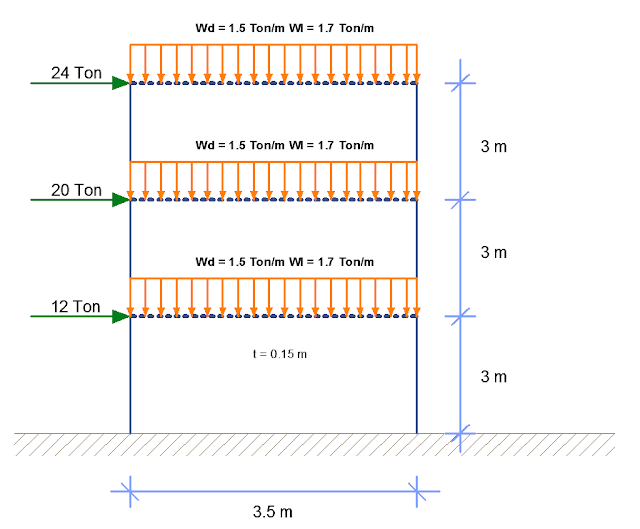
Diseñar el refuerzo necesario para el muro de corte que se muestra en la figura para resistir a las cargas sometidas. La altura de entrepiso es de 3m. usar f´c = 280 Kg/cm2 y fy = 4200 Kg/cm2, considerar que las cargas laterales son debidas a solicitaciones sísmicas y que el muro está apoyado en las losas de entrepiso mostradas con líneas punteadas en el gráfico.

Hallando las fuerzas internas en la base:

Para el diseño por compresión se usara el método empírico para determinar la resistencia del muro de concreto a la compresión, ya que la carga distribuida en él está centrada la resistencia será:

ϕPnw = 0.55x0.65x280x15x350x(1-(1x300/32x15))²) = 320242 Kg > 36750 Kg

el muro no requiere refuerzo por compresión. El factor de longitud efectiva es igual a 1 ya que el caso más desfavorable es el que corresponde al muro apoyado arriba y abajo sin restricción al giro en estos apoyos.

Para el diseño por flexión se debe encontrar el peralte efectivo de la sección que se estima como:

d= 0.8x3.5 = 2.8 m

También se debe verificar que el muro se pueda diseñar como un elemento esbelto, lo cual depende de la relación entre el peralte efectivo y su altura.

d/h = 2.8/9 = 0.31 < 0.4

Se debe diseñar el elemento como muro esbelto:

Ru = 37200000/(15x280)² = 31.63

Ρ = 0.91%

As = 0.91/100x280x15 = 38.22 cm²

Para el acero requerido se colocaran 14 varillas de 3/4” en cada extremo del muro.

Para el diseño por cortante verificar que la fuerza cortante en el elemento no sea mayor que la máxima permitida.

Vumax = 2.7x16.7x280x1 = 189378 Kg = 190 Ton

Vu/ϕ = 56/0.6) 74.7 Ton < Vumax

La resistencia a la corte aportada por el concreto en la sección ubicada a L/2 de la base (menor que H/2) es determinada a través de:

Vc = 0.88x16.7x15x280 + (36750x280)/(4x350) = 69073 Kg = 69.1 Ton

Vc = (0.16x16.7+350x (0.33x16.7+0.2x36750/(350x15))/(37200000/56000-350/2)) x15x280 = 31986 Kg = 32 Ton

El valor de Mu se determina:

Mu = 1x(24x(9-1.75) + 20x(6-1.75) + 12x(3-1.75)) = 274 Ton.m

Considerando la resistencia al corte más desfavorable:

ϕVc = 0.75x32 = 24 Ton

La resistencia al corte que debe ser aportada por el acero es:

Vs = (Vu-ϕVc)/ ϕ = (56000-24000)/0.75 = 42667 Kg

Para el refuerzo Horizontal:

Avh/s2 = 42667/4200/280 = 0.036

Para el acero requerido se necesita 2 varillas de 3/8” @ 35 cm para lo cual la cuantía:

ρ = 1.42/(35x15) ) 0.0027> ρmin = 0.0025

El espaciamiento máximo recomendado es:

Smax = L/5 = 0.70 m > 0.35m

Smax = 3h = 3x0.15 = 0.45m > 0.35 m

El refuerzo vertical del muro se calcula:

Ρn = 0.0025 + 0.5(2.5-9/3.5)x(1.42/35/15-0.0025) = 0.0025

Av = 0.0025x100x15 = 3.75cm²/m

El refuerzo vertical consistirá en 2 varillas de 3/8” @0.35